UNIST 이석형 교수, 양자역학과 상대성이론을 잇는 새로운 수학적 틀 제시
UNIST는 22일, 물리학과 이석형 교수가 양자역학과 상대성이론의 오래된 이론적 불일치를 해결할 수 있는 새로운 수학적 틀을 정립했다고 밝혔다. 이 교수는 시간에 걸쳐 일어나는 양자 동역학 전체를 하나의 양자상태로 기술하는 이론을 제안했으며, 해당 연구는 물리학 분야 최고 권위 학술지 중 하나인 Physical Review Letters에 게재됐다.
양자역학과 상대성이론은 현대 물리학을 떠받치는 두 기둥이지만, 공간과 시간을 바라보는 관점에서는 끝내 하나로 묶이지 못했다. 상대성이론이 공간과 시간을 하나의 ‘시공간’으로 다루는 반면, 양자역학은 공간에 대해서만 양자상태를 정의하고 시간은 변화가 일어나는 ‘과정’으로 취급해왔기 때문이다. 이번 연구는 이 오래된 이론적 비대칭을 정면으로 다룬 시도로 평가된다.
왜 ‘시간의 양자화’가 문제였을까
일반적으로 양자이론에서 공간상의 상관관계는 ‘양자상태’로, 시간에 따른 변화는 ‘양자채널’이나 ‘과정’으로 설명된다. 여기서 양자상태란 어떤 양자계가 관측될 확률을 결정하는 수학적 객체이고, 과정은 그 상태가 시간에 따라 어떻게 바뀌는지를 나타낸다. 이 구분은 계산에는 편리했지만, 시간과 공간을 대칭적으로 다루는 상대성이론과 결합하려 할 때 근본적인 한계로 작용해왔다.
이러한 문제의식에서 출발한 개념이 ‘시간상의 양자상태(Quantum State Over Time)’다. 이는 시간에 따라 이어지는 여러 양자 과정을 하나의 상태로 다루려는 시도다. 그러나 지금까지의 이론은 두 시점 사이의 경우에만 명확히 정립돼 있었고, 여러 단계로 이어지는 다시점(multipartite) 상황에서는 표현 방식이 유일하지 않다는 문제가 남아 있었다. 복잡한 동역학을 다루는 데 결정적인 걸림돌이었던 셈이다.
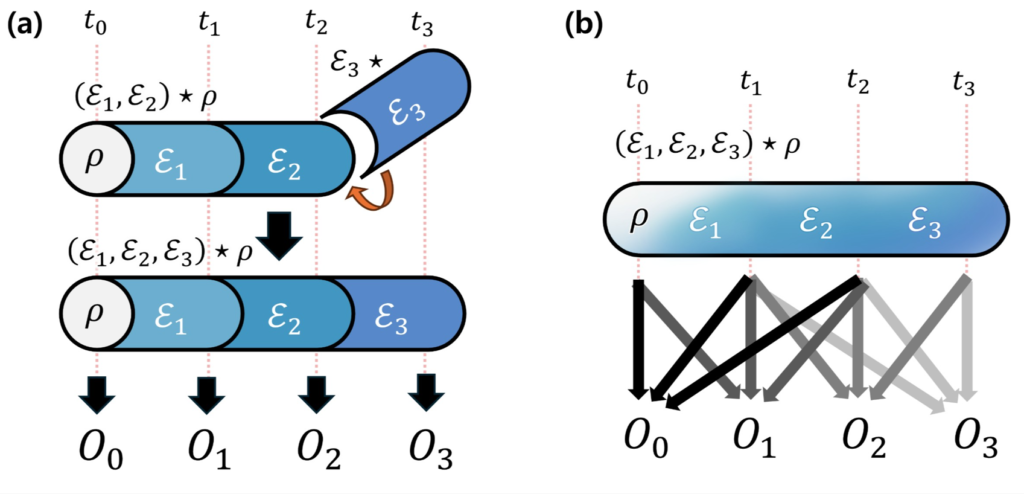
(a) 마르코브적 확장: 시간 상관관계를 단계별로 순차 확장한다. 실험에서도 한 단계씩 양자상태를 복원할 수 있어 계산과 측정이 효율적이다.
(b) 전체론적 확장: 모든 시점을 한꺼번에 묶어 계산한다. 순차 확장이 불가능해 단일 물리량을 얻기 위해서도 전체 시간 데이터가 필요해 비효율적이다.
시간을 하나의 상태로 묶는 방법
이석형 교수 연구의 핵심은 여러 시점에서 일어나는 양자 동역학 전체를 하나의 ‘거대한 양자상태’로 묶는 데 있다. 연구진은 이를 ‘시간 위의 다자 양자상태’라고 부른다. 공간적으로 떨어진 계를 하나의 수학 구조로 다루듯, 시간적으로 떨어진 계 역시 동일한 방식으로 다룰 수 있다는 발상이다.
이를 위해 연구진은 물리적으로 자연스러운 두 가지 기본 가정만을 세우고 출발했다. 그리고 이 조건을 만족하는 시간 양자상태의 수학적 구조가 단 하나로 결정된다는 사실을 증명했다. 다시 말해, 여러 해석 중 하나를 선택한 것이 아니라, 주어진 조건에서는 다른 선택지가 없다는 점을 수학적으로 보여준 것이다. 이때 도출된 구조는 ‘마르코브 과정’—즉, 현재 상태가 바로 직전 상태에만 의존하고 그 이전의 기억을 갖지 않는 과정—에 해당하며, 시간상의 양자상태 역시 단계별로 분리되는 ‘양자 마르코브 체인’ 형태를 갖게 된다.
이 이론은 또 하나의 중요한 연결고리를 제시한다. 시간상의 양자상태가 커크우드-디랙 준확률분포와 일대일로 대응한다는 점을 밝힌 것이다. 준확률분포란 음수나 복소수 값도 허용하는 확장된 확률 개념으로, 양자중첩이나 얽힘처럼 고전 확률로는 설명하기 어려운 현상을 기술하는 데 사용된다. 이 대응 관계 덕분에, 시간에 따른 양자 상관관계는 약한 측정과 같은 실험 기법을 통해 실제로 관찰 가능해진다.
이론적 의미도 분명하다. 연속적인 양자계 모니터링이나 양자계측에서는 수학적 표현이 크게 단순화되고, 더 나아가 시간과 공간을 동등하게 양자화하려는 시도—양자역학과 상대성이론을 완전히 결합하려는 연구—에 필요한 기초 도구로 활용될 수 있다.
이석형 교수는 이번 연구가 “시간과 공간을 하나의 양자 언어로 기술하기 위한 첫걸음 중 하나”라고 설명한다. 공간에만 머물러 있던 양자상태의 개념을 시간으로 확장한 이 시도는, 물리학이 오랫동안 피해왔던 질문을 다시 정면으로 불러내고 있다.